In the last blog we had discussed about monte carlo methods and temporal difference methods which are used to preform reinforcement learning in unknown MDP enviorment. We also learnt about Q-Learning which is an off-policy Temporal Difference control method. In this blog, we will understand some of the limitation of traditional Q-Learning and will learn about Deep Q-Learning and will also build a Flappy Bird Reinforcement Learning agent with some advanced Deep Q Networks. Before that, if you dont know what Q Learning is or have no idea about reinforcement learning, please checkout my last blog (below link).

Monte Carlo and Temporal Difference Learning in an Unknown MDP environment.

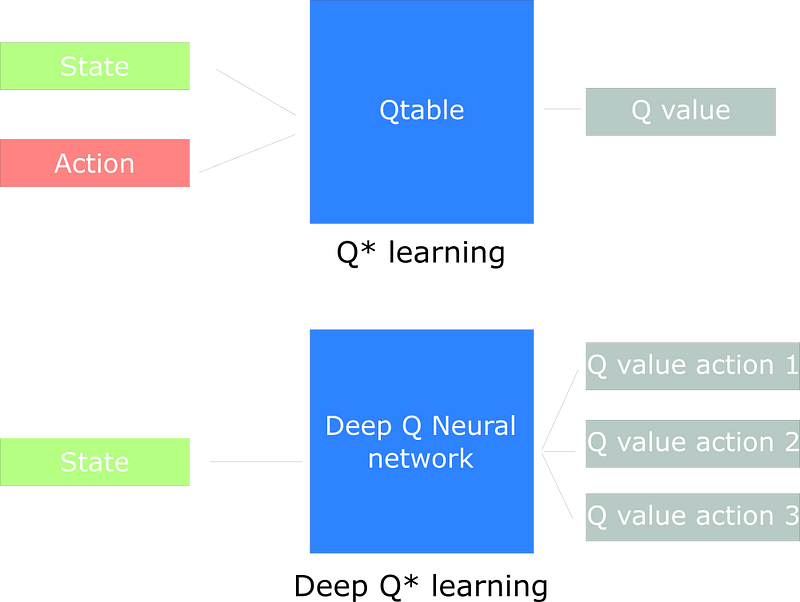
Q-Learning is an off-policy Learning which is a development over on-policy TD control i.e. SARSA. Q-learning tries to estimate a state-action value function for target policy that deterministically selects the action of highest value. Q-Learning in the end produces a Q-table "a cheat-sheet" that an agent uses to find the best action to take given a state.

Limitations of Q - Learning:

1. Producing and updating a Q-table can become ineffective in big state space environments.
2. In the enviroments where there is no discrete states and there are continuous values represnting state of environment. Then it is not possible to use traditional Q-Learning.

Deep Q-Learning :

Q-table is a good strategy — however, this is not scalable. Instead of using a Q-table, we’ll implement a Neural Network that takes a state and approximates Q-values for each action based on that state. Imagine any GTA game where an agaent can be millions of state and making a Q-table for them would not be efficient at all. The best idea in this case is to create a neural network that will approximate, given a state, the different Q-values for each action.



For the reinforcement learning agent for flappy bird game our deep Q Network will work like this:

We will stack 4 frames of game in one array and this will act as a input the neural network. We will use four frames because with one frame our network can get confused whether the bird is going down or up but giving four frames will help in determine current movement of bird. The output of the neural network will be vector of Q values which correspond to each action that an agent can take. Here, in flappy bird game the output vector has size of 2 as their are 2 actions, either go up (flap) or do nothing (which will take bird down). We will pick the action with biggest Q value.

For our flappy bird agent we will use convolutional neural networks because they excel in solving problems which involves images. We will provide this convolutional network 4 greyscale frames with some extra preprocessing (we'll discuss later). Colorful images does not add extra value to the input but also takes extra computation power.

As we play the game we will store our experiences in a buffer say experience buffer and we will sample a batch of experience from time to time to train our deep neural network. We will also keep on removing older experiences as they will later not add value to the training also but also end up taking extra memory. Here will sample a batch uniformly means every experience has a equal weightage of getting picked up for training. Later we will implement Prioritized Experience Replay in which we will assign more priority to some experience.

Here I will perform an action 2 times means I will skip 2 frames performing same action. This is because there are so many non important frame and using all frame to select and action will take so much time and will be redundant in out experience buffer. It looks like skipping one or two frames after an action doesn't affect our training in drastic way.

Training the model

To the train our Neural Network we will use adam optimizer for minimize the mean squared error loss. When we perform a step in the environment we will it will return 3 variables i.e. next frame, rewards, done. Here done represent whether the game has ended or not. Here we will use 2 copies of Neural Network and it is called Double DQN. We will update target DQN after some time steps in game. To calculate the loss, we need 2 values the current state action value and expected state action value.

We will calculate expected state action (TD target) value as follows from the target DQN: $$ \text{state-action-value}_t = reward_t + \gamma * max_a (\text{state-action-value}_{t+1}) $$ and current state action value is calculated from current DQN. The mean squared error loss is calculated using these 2 values for each sample in batch. Also we must take care of next state-action value if the episode has ended, if the episode has ended then make next state-action value as 0.

Dueling DQN Architecture

Remember that Q-values correspond to how good it is to be at that state and taking an action at that state Q(s,a).
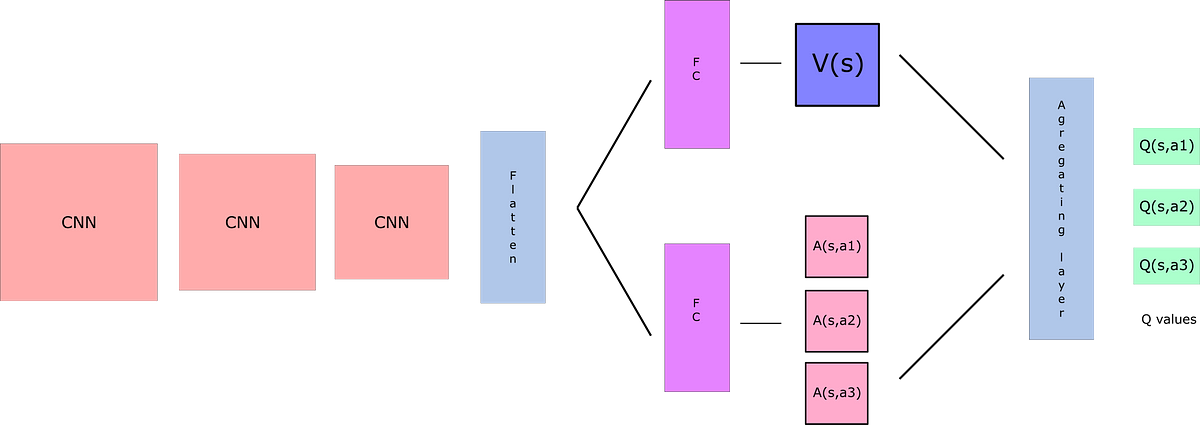
So we can decompose Q(s,a) as the sum of:
V(s): the value of being at that state
A(s,a): the advantage of taking that action at that state (how much better is to take this action versus all other possible actions at that state)
$$ Q(s,a) = V(s) + \Big( A(s,a) - mean_{a \in A}(A(s,a)) \Big) $$
Wait? But why do we need to calculate these two elements separately if then we combine them?
By decoupling the estimation, intuitively our DDQN can learn which states are (or are not) valuable without having to learn the effect of each action at each state (since it’s also calculating V(s)).
With our normal DQN, we need to calculate the value of each action at that state. But what’s the point if the value of the state is bad? What’s the point to calculate all actions at one state when all these actions lead to death?
As a consequence, by decoupling we’re able to calculate V(s). This is particularly useful for states where their actions do not affect the environment in a relevant way. In this case, it’s unnecessary to calculate the value of each action. For instance, moving right or left only matters if there is a risk of collision. And, in most states, the choice of the action has no effect on what happens.

Prioritized Experience Replay

The idea behind PER is that some experiences may be more important than others for our training, but might occur less frequently. Because we sample the batch uniformly (selecting the experiences randomly) these rich experiences that occur rarely have practically no chance to be selected. We want to take in priority experience where there is a big difference between our prediction and the TD target, since it means that we have a lot to learn about it.
We use the absolute value of the magnitude of our TD error: $$ p_t = | \partial | + e $$ Here,
`p_t` : Priority Value
`| \partial |` : magnitude of TD error
` e ` : constant assures priority do not become zero
Now, we will calulate probability of being choosen: $$ P(i) = \frac{p^a_i}{ \sum_k p^a_k} $$

Click to view all code.

More Resources

1. Introduction to Deep Q Learning
2. Improvements in Deep Q Learning
3. Prioritized Experience Replay by Google Deep Mind
4. Jaromiru's blog about LET’S MAKE A DQN